Por Que a Significância Estatística é Importante?
Descubra por que a significância estatística é fundamental na análise de dados, pesquisas e decisões de negócios. Saiba sobre p-valores, testes de hipótese e co...
Descubra como a significância estatística determina se resultados são reais ou fruto do acaso. Entenda p-values, testes de hipóteses e aplicações práticas para o seu negócio em 2025.
A significância estatística é utilizada para determinar se um resultado ocorreu por acaso ou foi causado por algum fator de interesse. Se for estatisticamente significativo, é improvável que tenha ocorrido aleatoriamente.
A significância estatística é um conceito fundamental na análise de dados que ajuda você a diferenciar entre efeitos genuínos e flutuações aleatórias nos seus dados. Ao realizar experimentos, pesquisas ou analisar métricas de negócios, é necessário um método confiável para determinar se os padrões observados são reais ou simplesmente resultado do acaso. A significância estatística fornece esse arcabouço crítico ao usar princípios matemáticos para avaliar a probabilidade de seus resultados terem ocorrido caso realmente não houvesse efeito ou diferença entre os grupos comparados.
O conceito surgiu a partir do trabalho do estatístico Ronald Fisher no início do século XX e tornou-se a base dos testes de hipóteses em praticamente todas as áreas que utilizam análise de dados. De pesquisas farmacêuticas validando novos tratamentos a empresas de e-commerce otimizando taxas de conversão, a significância estatística atua como guardiã entre insights acionáveis e conclusões enganosas. Entender como a significância estatística funciona capacita você a tomar decisões informadas, respaldadas por evidências sólidas em vez de intuição ou coincidência.
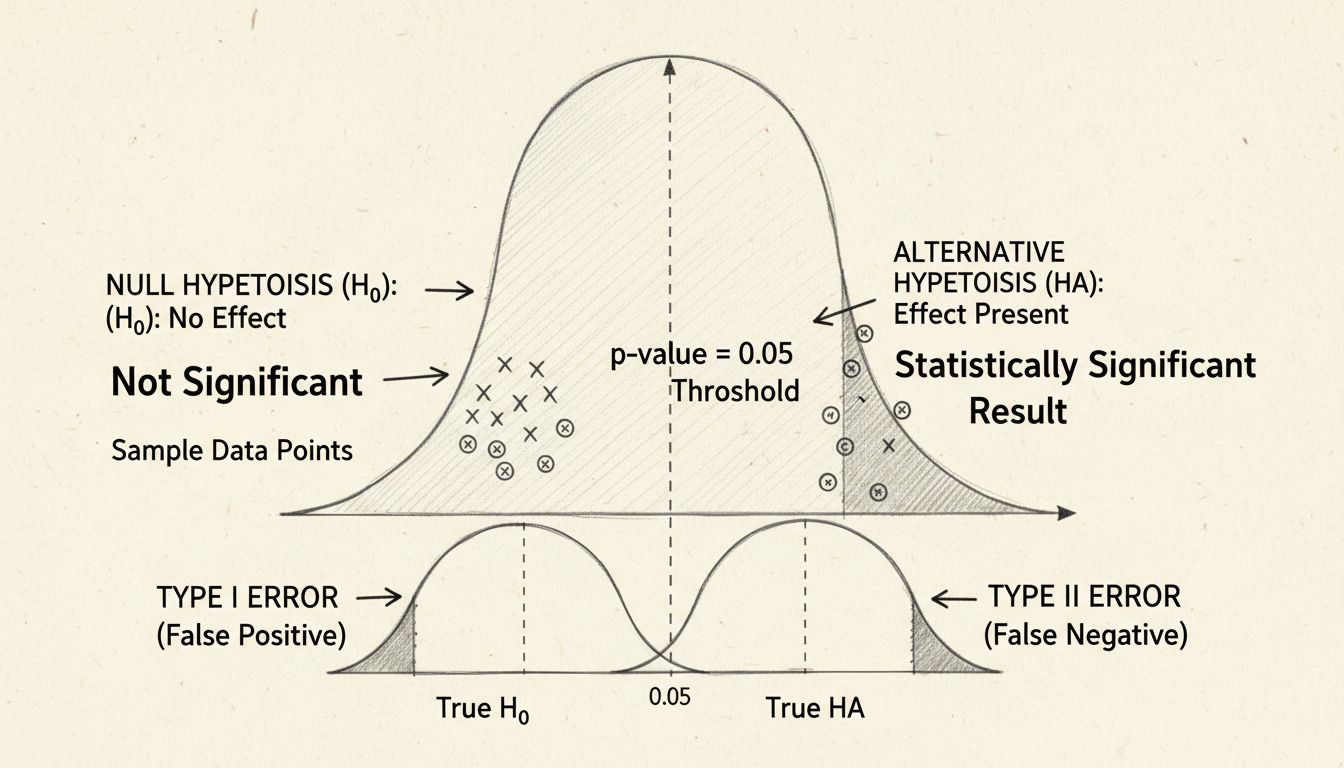
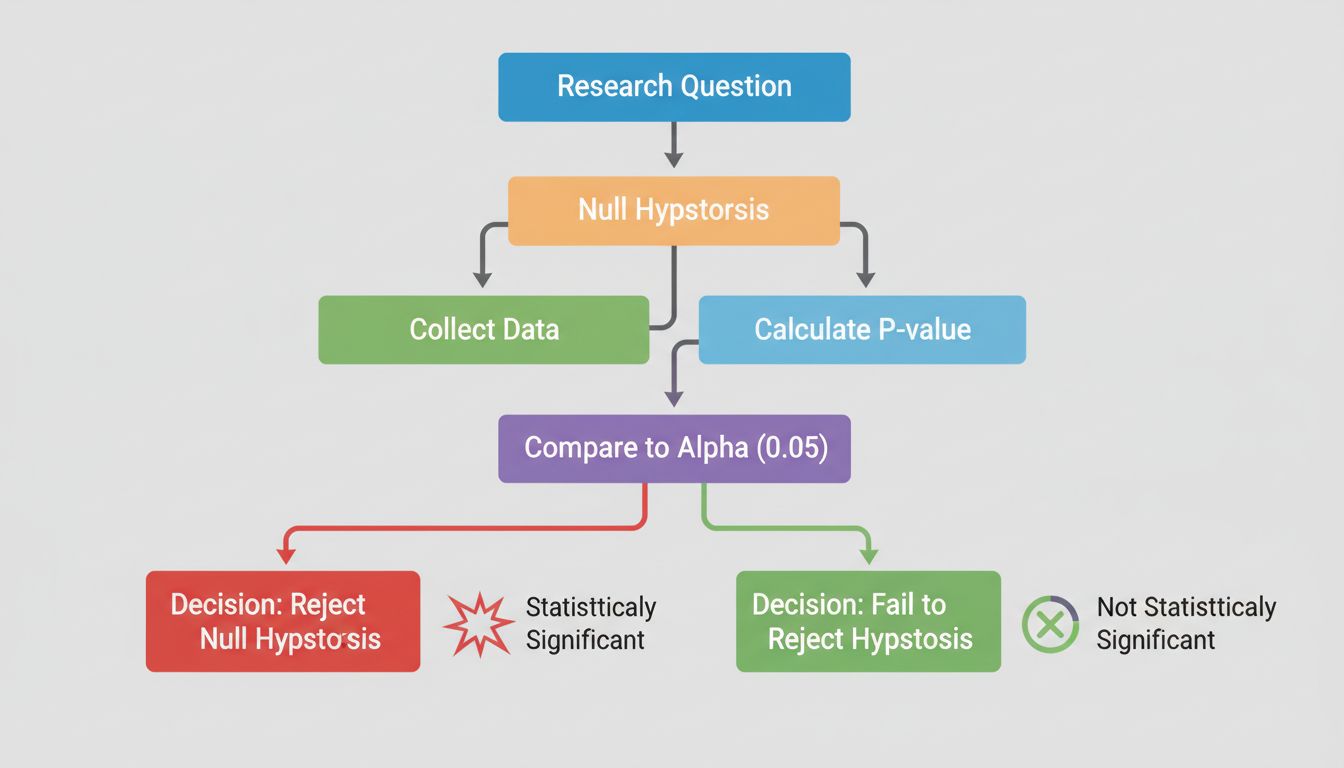
No coração da significância estatística está o teste de hipóteses, uma metodologia estruturada para avaliar afirmações sobre seus dados. O processo começa com a formulação de duas hipóteses concorrentes: a hipótese nula e a hipótese alternativa. A hipótese nula assume que não há efeito real ou diferença entre os grupos estudados — essencialmente, representa o status quo ou a suposição de que qualquer diferença observada é puramente devido ao acaso. Já a hipótese alternativa propõe que existe sim um efeito ou diferença real.
Considere um exemplo prático: você está testando se uma nova campanha de marketing de afiliados gera taxas de conversão mais altas do que a abordagem atual. Sua hipótese nula afirmaria que ambas as campanhas produzem taxas de conversão idênticas, enquanto a hipótese alternativa alegaria que a nova campanha apresenta desempenho diferente. O teste estatístico então avalia qual hipótese os dados sustentam mais fortemente. Esse arcabouço impede que pesquisadores e analistas selecionem resultados que apenas confirmam suas expectativas; em vez disso, obriga a provar que suas descobertas dificilmente ocorreram por acaso.
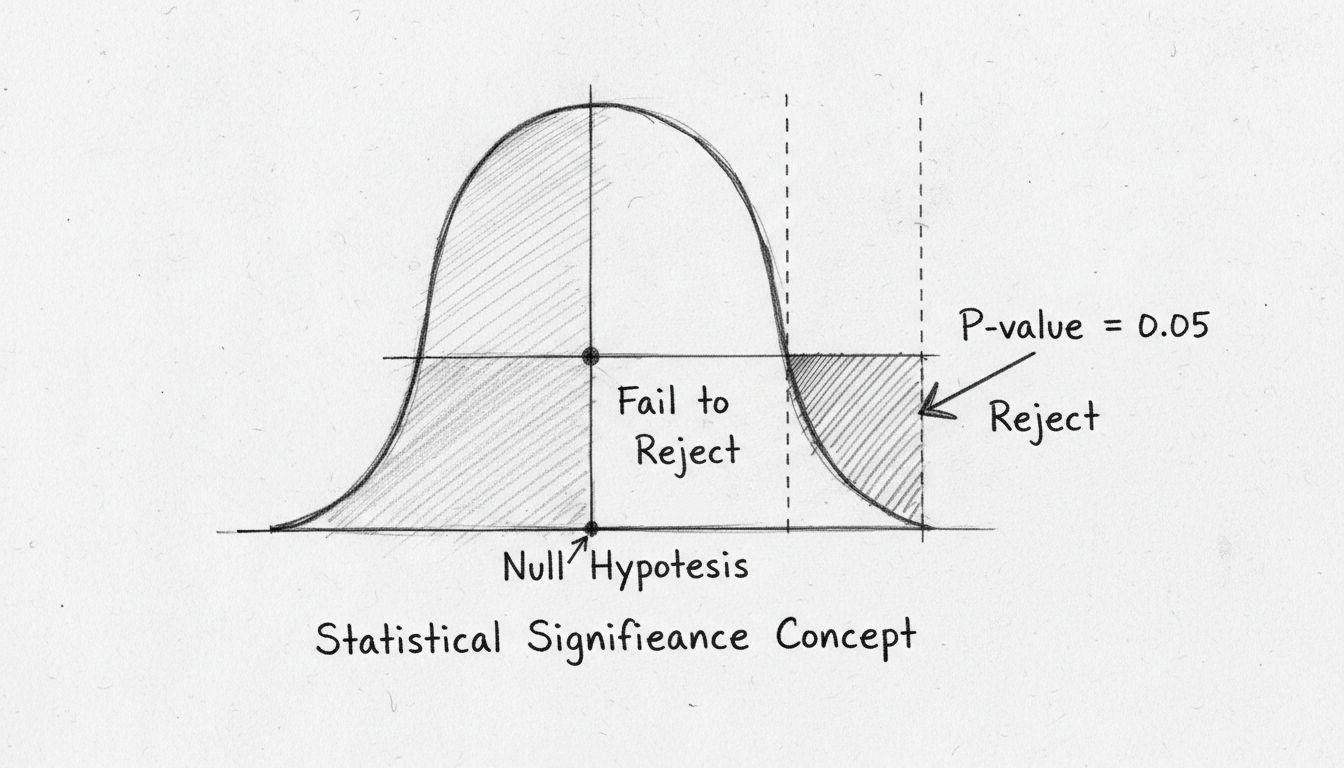
A beleza do teste de hipóteses está em sua objetividade. Em vez de depender de julgamentos subjetivos, você utiliza cálculos matemáticos para determinar se os dados fornecem evidências suficientes para rejeitar a hipótese nula. Se a evidência for forte o suficiente, é possível afirmar com confiança que o efeito observado é estatisticamente significativo — ou seja, é improvável que seja um acaso.
O p-valor talvez seja a métrica mais utilizada nos testes de significância estatística, embora seja frequentemente mal compreendida. O p-valor representa a probabilidade de observar seus resultados (ou resultados ainda mais extremos) caso a hipótese nula seja verdadeira. Em outras palavras, responde à pergunta: “Qual a chance de eu ver esses dados se realmente não houver efeito?” Um p-valor pequeno indica que os resultados observados seriam muito improváveis sob a hipótese nula, sugerindo que ela provavelmente é falsa e o seu efeito, real.
O limite convencional para significância estatística é um p-valor de 0,05 ou menos, o que corresponde a uma probabilidade de 5% de os resultados terem ocorrido por acaso. Significa que você aceita um risco de 5% de rejeitar incorretamente a hipótese nula quando ela na verdade é verdadeira (chamado de erro do Tipo I). No entanto, esse limite é um tanto arbitrário e varia conforme o campo e o contexto. Em pesquisas médicas, onde as consequências de falsos positivos podem ser graves, geralmente se adota um limite mais rígido, como 0,01 (1%). Por outro lado, em pesquisas exploratórias ou testes iniciais, um limite de 0,10 (10%) pode ser aceitável.
| Faixa do P-Valor | Interpretação | Ação Típica |
|---|---|---|
| p < 0,01 | Altamente significativo | Forte evidência contra a hipótese nula |
| 0,01 ≤ p < 0,05 | Significativo | Evidência moderada contra a hipótese nula |
| 0,05 ≤ p < 0,10 | Marginalmente significativo | Evidência fraca contra a hipótese nula |
| p ≥ 0,10 | Não significativo | Evidência insuficiente para rejeitar a hipótese nula |
É fundamental entender o que um p-valor não indica. Um p-valor de 0,03 não significa que há 97% de chance de sua hipótese ser verdadeira. Também não mede o tamanho ou a importância prática do seu efeito. Um resultado estatisticamente significativo pode ainda representar um efeito trivialmente pequeno, sem impacto real. Esta distinção entre significância estatística e significância prática é uma das fontes mais comuns de confusão em análise de dados.
Enquanto os p-valores indicam se um efeito existe, os intervalos de confiança fornecem informações cruciais sobre a magnitude e a precisão desse efeito. Um intervalo de confiança é um intervalo de valores que provavelmente contém o tamanho real do efeito, calculado com um nível de confiança especificado (normalmente 95%). Se você está testando se um novo recurso do programa de afiliados aumenta as comissões, um intervalo de confiança de 95% pode indicar que o aumento real está entre 2% e 8%, com 95% de confiança de que o valor verdadeiro está dentro desse intervalo.
Os intervalos de confiança oferecem várias vantagens sobre apenas os p-valores. Primeiro, comunicam tanto a direção quanto a magnitude do efeito, proporcionando uma visão mais completa dos resultados. Segundo, ajudam a avaliar a significância prática — mesmo que um efeito seja estatisticamente significativo, se o intervalo de confiança mostrar que o efeito é insignificante, pode não justificar a implementação. Terceiro, intervalos de confiança estreitos indicam estimativas precisas, enquanto intervalos largos sugerem maior incerteza nos achados.
Tamanho do efeito mede a força da relação entre variáveis ou a magnitude da diferença entre grupos. Medidas comuns de tamanho de efeito incluem d de Cohen (para comparação de médias), coeficientes de correlação e razões de chances (odds ratio). Um efeito pode ser estatisticamente significativo, mas ter tamanho pequeno, ou seja, impacto prático mínimo. Por outro lado, um tamanho de efeito grande pode não atingir significância estatística se a amostra for pequena. Analistas profissionais sempre relatam tamanhos de efeito junto com p-valores para oferecer um panorama completo de suas descobertas.
O tamanho da amostra tem papel crucial na determinação da significância estatística. Amostras maiores oferecem mais informações sobre a população e reduzem o impacto das variações aleatórias, facilitando a detecção de efeitos reais. Por outro lado, amostras pequenas são mais suscetíveis a flutuações aleatórias, podendo levar tanto a falsos positivos (detectar um efeito inexistente) quanto falsos negativos (não detectar um efeito existente).
A relação entre tamanho da amostra e poder estatístico é fundamental no desenho de pesquisas. Poder estatístico é a probabilidade de rejeitar corretamente a hipótese nula quando ela é falsa — ou seja, sua capacidade de detectar um efeito real. A maioria dos pesquisadores busca um poder de 0,80 (80%), aceitando um risco de 20% de não detectar um efeito real. Para atingir esse nível de poder, é preciso um tamanho de amostra suficientemente grande, o que depende do tamanho de efeito esperado, do nível de significância escolhido e do tipo de teste estatístico utilizado.
Antes de realizar qualquer estudo ou experimento, pesquisadores devem conduzir uma análise de poder para determinar o tamanho de amostra necessário. Isso evita desperdiçar recursos em estudos pequenos demais para detectar efeitos relevantes, além de impedir estudos excessivamente grandes e custosos. No contexto do marketing de afiliados, isso significa saber quantas conversões ou cliques precisam ser observados antes de concluir com confiança que uma mudança em campanha teve impacto real.
Diferentes perguntas de pesquisa e tipos de dados exigem testes estatísticos distintos. A escolha do teste depende de fatores como número de grupos comparados, se os dados têm distribuição normal, se as amostras são independentes ou pareadas e o tipo de variável de desfecho (contínua, categórica, etc.).
O teste t de Student compara as médias de dois grupos e é um dos testes mais utilizados. É adequado para dados contínuos (como valores de receita) quando se deseja saber se dois grupos diferem significativamente. O teste leva em conta a variabilidade dentro de cada grupo e os tamanhos das amostras, produzindo um t-estatístico que é comparado a um valor crítico para determinar a significância.
O teste qui-quadrado é utilizado para dados categóricos, para verificar se as frequências observadas diferem significativamente das esperadas. Se você está analisando se o canal de afiliado (email, redes sociais, banners) afeta as taxas de conversão, o teste qui-quadrado é apropriado.
A ANOVA (Análise de Variância) estende o teste t para comparar médias entre três ou mais grupos simultaneamente. Isso evita o problema de múltiplas comparações, onde a realização de vários testes separados aumenta a chance de falsos positivos.
O teste de Mann-Whitney U e o teste de Wilcoxon são alternativas não paramétricas usadas quando os dados não atendem aos pressupostos dos testes paramétricos, como ausência de distribuição normal.
No mundo dos negócios, a significância estatística orienta decisões críticas em diversas funções. Equipes de marketing usam testes A/B com significância estatística para determinar se mudanças em sites, assuntos de email ou criativos de anúncios realmente melhoram as métricas de desempenho. Ao invés de confiar em intuição ou pequenas amostras, empresas orientadas por dados estabelecem limites de significância antes dos testes, garantindo que as decisões sejam baseadas em evidências confiáveis.
No marketing de afiliados especificamente, a significância estatística ajuda a identificar quais afiliados, campanhas e estratégias promocionais realmente geram receita, em vez daquelas que parecem bem-sucedidas por variação aleatória. Ao avaliar se uma nova estrutura de comissão aumenta o desempenho dos afiliados, o teste estatístico impede mudanças caras baseadas em flutuações de curto prazo. A plataforma avançada de analytics da PostAffiliatePro permite acompanhar métricas de afiliados com o rigor estatístico necessário para decisões de otimização confiáveis.
Na pesquisa farmacêutica e médica, a significância estatística determina se novos tratamentos são eficazes o bastante para aprovação e uso. Ensaios clínicos precisam demonstrar que o benefício de um medicamento é estatisticamente significativo antes de ser prescrito a pacientes. Os riscos são altos, por isso a pesquisa médica geralmente utiliza níveis de significância mais rigorosos que outros campos.
Um dos equívocos mais comuns é achar que significância estatística prova causalidade. Uma correlação estatisticamente significativa entre duas variáveis não significa que uma causa a outra. O exemplo clássico é a forte correlação entre lançamentos de filmes do Nicolas Cage e afogamentos em piscinas — claramente, um não causa o outro. A significância estatística apenas indica que uma relação é improvável de ser fruto do acaso; estabelecer causalidade exige evidências adicionais, como mecanismo lógico, ordem temporal e experimentos controlados.
Outro erro comum é o p-hacking ou garimpagem de dados, quando se realizam inúmeros testes estatísticos no mesmo conjunto de dados até encontrar resultados significativos. Essa prática aumenta artificialmente a chance de falsos positivos, pois com testes suficientes, inevitavelmente algo será significativo por acaso. Se forem feitos 20 testes independentes com nível de 0,05, espera-se um falso positivo só pelo acaso. Pesquisadores responsáveis predefinem hipóteses e testes estatísticos antes da análise, prevenindo esse problema.
Outra armadilha é interpretar incorretamente resultados não significativos. Um resultado não significativo não prova que não há efeito; apenas significa que não há evidência suficiente para rejeitar a hipótese nula. Isso pode dever-se a amostra insuficiente, alta variabilidade nos dados ou ausência real de efeito. Ausência de evidência não é evidência de ausência.
A estatística continua evoluindo, com reconhecimento crescente das limitações dos métodos tradicionais baseados em p-valor. Muitos estatísticos defendem uma abordagem mais sofisticada, que combine p-valores com tamanhos de efeito, intervalos de confiança e métodos bayesianos. A estatística bayesiana, que incorpora conhecimento prévio e atualiza crenças com base nos dados observados, oferece um arcabouço alternativo que alguns consideram mais intuitivo e flexível do que o frequencista.
Testes sequenciais e desenhos adaptativos ganharam destaque, permitindo monitorar resultados à medida que os dados se acumulam e tomar decisões sobre continuar, modificar ou encerrar estudos com base em análises intermediárias. Essa abordagem é especialmente valiosa em negócios, onde decisões precisam ser tomadas rapidamente. Ferramentas como o Stats Engine da Statsig implementam testes sequenciais com controle da taxa de descobertas falsas, possibilitando decisões mais rápidas e precisas durante experimentos.
A crise de replicação na ciência também destacou a importância de entender corretamente a significância estatística. Muitas descobertas publicadas não se replicam, em parte porque pesquisadores e revistas focaram excessivamente em obter significância estatística, ignorando tamanhos de efeito e significância prática. No futuro, a ênfase está mudando para transparência, pré-registro de estudos e relato de todos os resultados, independentemente da significância.
Para usar a significância estatística de forma eficaz, defina seu nível de significância e o tamanho de amostra necessário antes da análise. Isso evita a tentação de ajustar limites depois de ver os resultados. Sempre relate tamanhos de efeito e intervalos de confiança junto com p-valores para fornecer um panorama completo dos achados. Considere a significância prática de seus resultados — um efeito estatisticamente significativo pode ser pequeno demais para ter relevância prática.
Seja transparente quanto à sua metodologia, incluindo como lidou com dados ausentes, outliers e múltiplos testes. Se realizou múltiplos testes, aplique correções apropriadas, como a correção de Bonferroni, para manter o nível geral de significância. Documente o processo de análise e esteja disposto a compartilhar seus dados e código para verificação e replicação.
Por fim, lembre-se de que a significância estatística é uma ferramenta, não um fim. Ela ajuda a tomar decisões melhores ao reduzir a influência do acaso, mas deve ser combinada com conhecimento do negócio, considerações práticas e julgamento estratégico. No marketing de afiliados, a significância estatística auxilia a identificar estratégias que realmente melhoram o desempenho, mas também é importante considerar custos de implementação, satisfação dos afiliados e sustentabilidade a longo prazo ao tomar decisões estratégicas.
As ferramentas avançadas de análise e relatórios da PostAffiliatePro ajudam você a acompanhar o desempenho dos afiliados com rigor estatístico. Descubra quais campanhas realmente geram resultados e otimize seu programa de afiliados com base em insights de dados confiáveis.

Descubra por que a significância estatística é fundamental na análise de dados, pesquisas e decisões de negócios. Saiba sobre p-valores, testes de hipótese e co...
A significância estatística expressa a confiabilidade dos dados medidos, ajudando empresas a distinguir efeitos reais do acaso e a tomar decisões informadas, es...
o significado estatístico em testes A/B para campanhas de afiliados de apostas.
See our privacy policy.